

 ,提醒大家 虽然比上周容易 但是也有一定难度大家不要投机取巧作弊,否则会给你大大的红叉!
,提醒大家 虽然比上周容易 但是也有一定难度大家不要投机取巧作弊,否则会给你大大的红叉!














 天啊~!
天啊~!

 ....
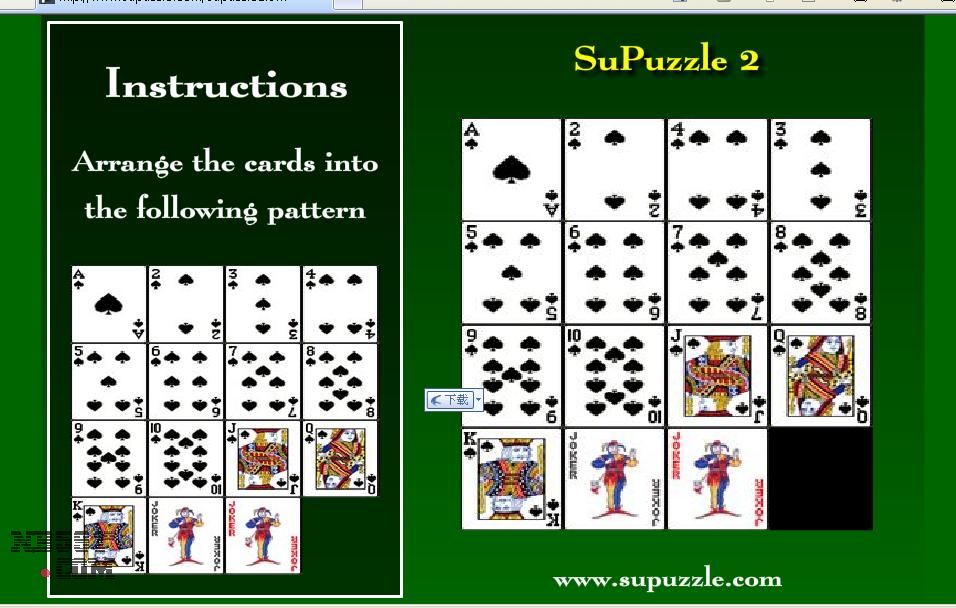
....
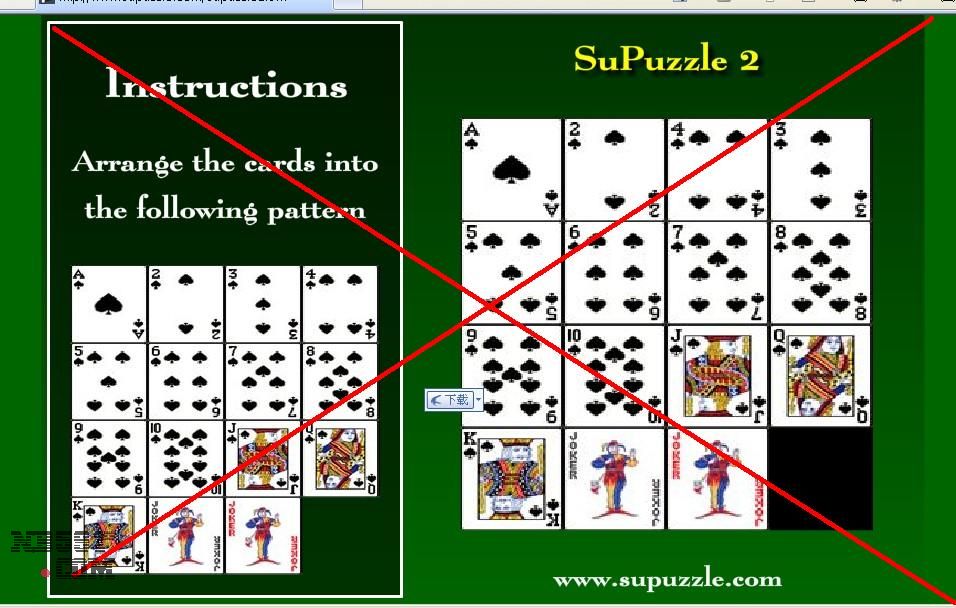


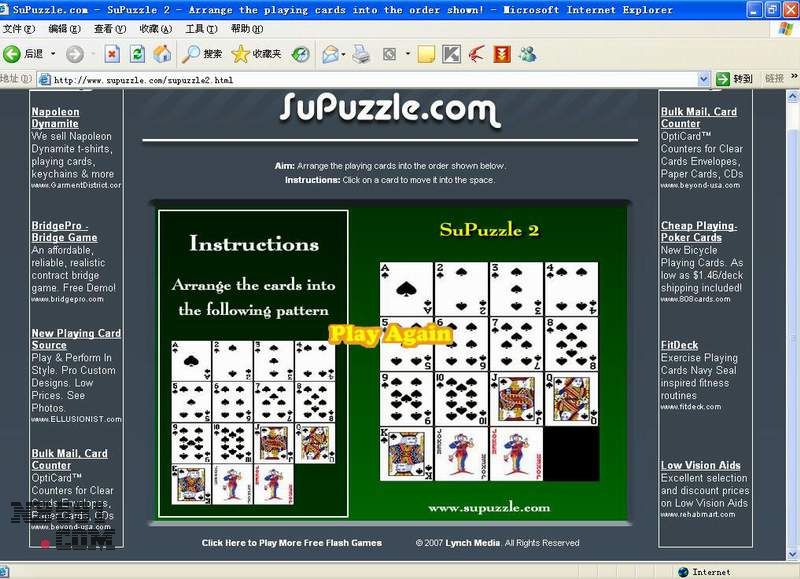

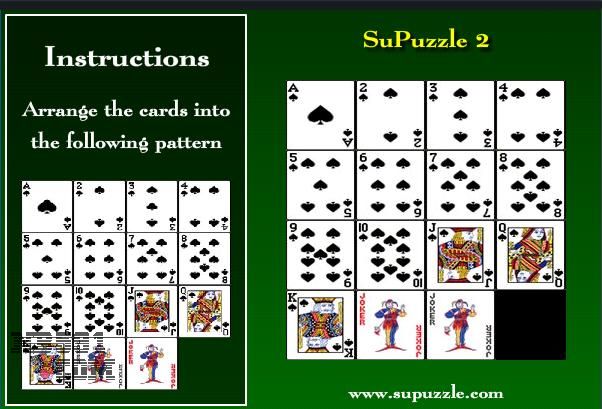
 最后两张。。。。弄不出来,LW给个帽子鼓励一下吧。
最后两张。。。。弄不出来,LW给个帽子鼓励一下吧。
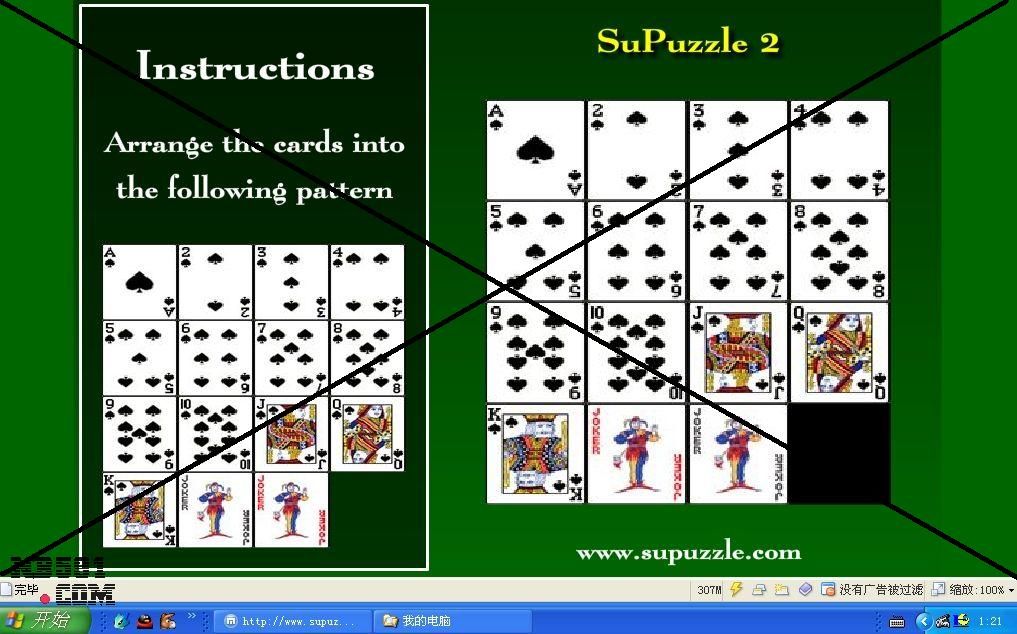










原帖由 MIKE_IBM 于 2007-9-14 23:08 发表
关于这题的无解的证明如下:
有人发现15-puzzle的状态可以均分为两个状态集:同一状态集中的
任意两个状态可以相互转换,非同一状态集的则不能。证明后一半不难,先从8-puzzle
开始,目标状态是:
1 2
...
| 欢迎光临 鸿利在线|北京Thinkpad水货|IBM水货|Thinkpad笔记本|Thinkpad全球购|Thinkpad美行|Thinkpad水货笔记本|Thinkpad港行笔记本|Thinkpad T14|X13|P15|P17|P1隐士| X1 Carbon 9代 |T14S|2021款X1 Carbon|X1 隐士|Thinkpad非官方论坛|Thinkpad工作站|Thinkpad笔记本论坛|Thinkpad水货 (http://hongmz.cn:8989/) | Powered by Discuz! 7.2 |