

 大家辛苦啦!
大家辛苦啦!











 ,没画出来
,没画出来


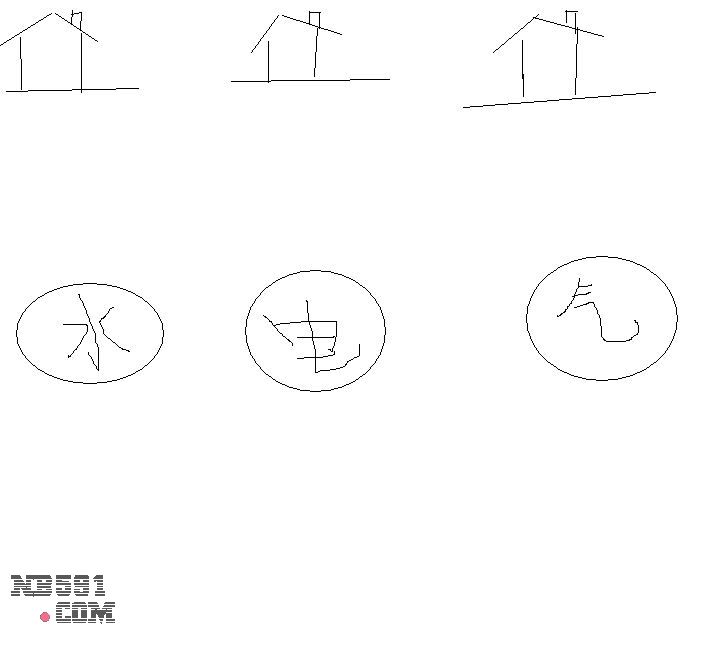
 You must draw a line from each house to each utility, without the lines ever crossing. Can you connect the houses to the utilities?
You must draw a line from each house to each utility, without the lines ever crossing. Can you connect the houses to the utilities? A piece of paper with a hole in it is like a torus that has been squashed flat. This means that the three utilities problem can also be solved by cutting a hole in the center of a piece of paper. Lines are allowed to go around the sides of the paper, or through the hole to the other side.
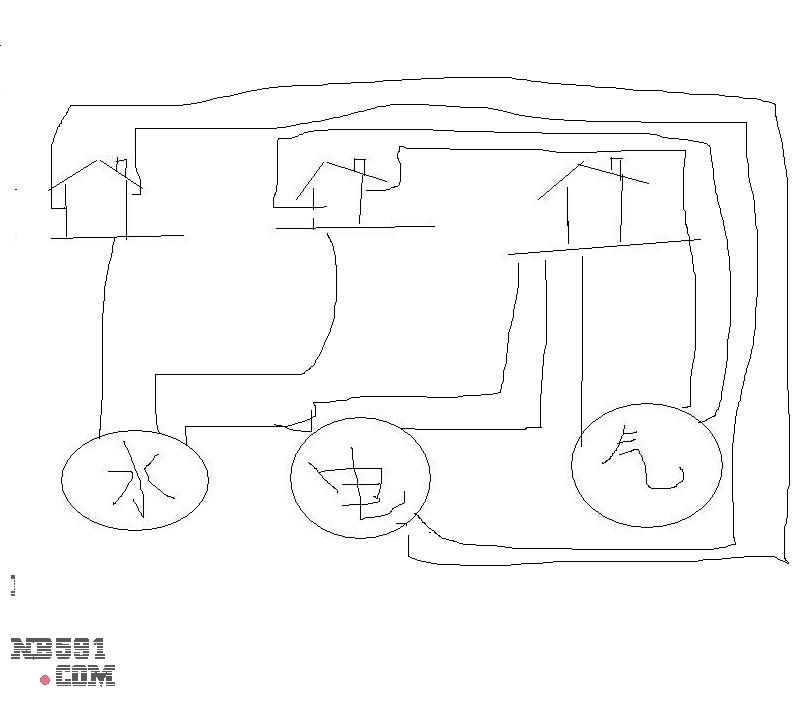
A piece of paper with a hole in it is like a torus that has been squashed flat. This means that the three utilities problem can also be solved by cutting a hole in the center of a piece of paper. Lines are allowed to go around the sides of the paper, or through the hole to the other side.| Let's start by drawing lines from some of the utilities to some of the houses: gas -> house 1 -> electricity -> house 2 -> water -> house 3. |  |
| If we draw one more line, from house 3 to the gas company, then we have a loop. Notice that our loop has an inside and an outside. |  |
| That means two lines will have to be either outside or inside the loop. These two lines will have to cross. |  |
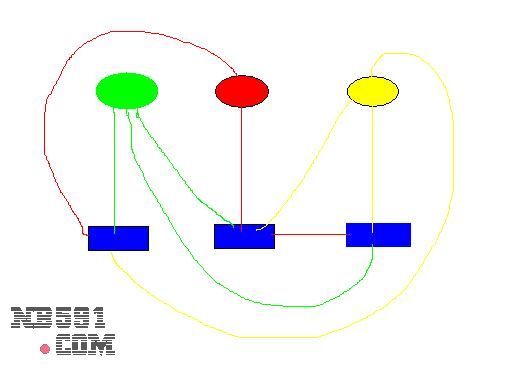
| That means the boundary of a face could either be house 1 - utility 1 - house 2 - utility 2 (four edges): |  |
| or house 1 - utility 1 - house 2 - utility 2 - house 3 - utility 3 (six edges): |  |


 :lol
:lol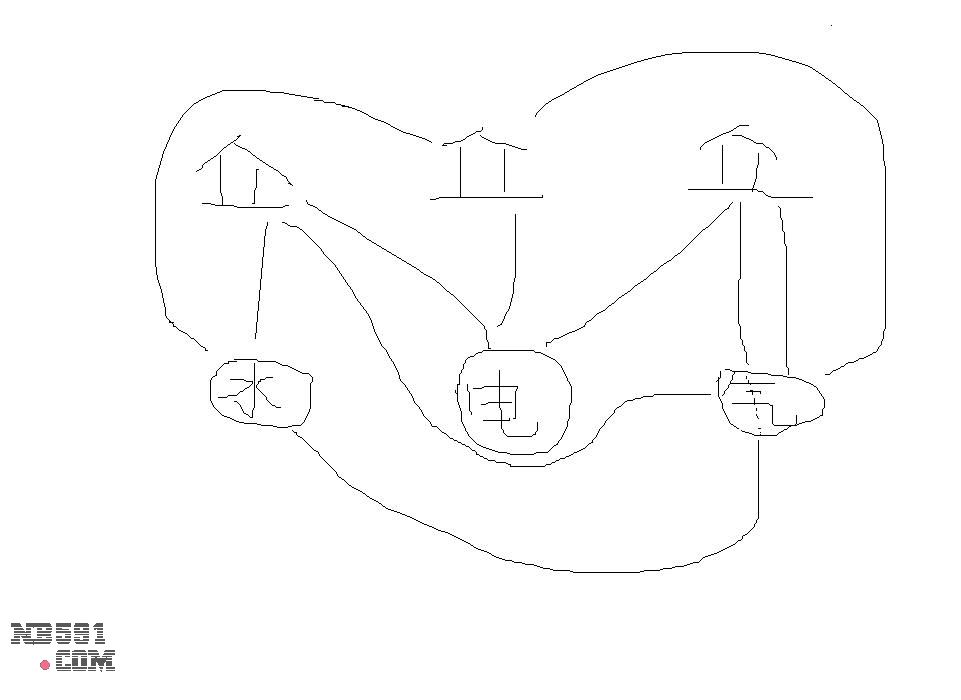










 老吴是天才!给个无解的题目!
老吴是天才!给个无解的题目!原帖由 pontifex 于 2007-9-7 12:32 发表
我给一个浅显一点的证明吧:拿出纸笔画一下.
把房子进行编号,叫做1,2,3;而水,电,气分别用A,B,C代替.
首先,只考虑1,2,A,B.可知这四个元素必然会连成一个封闭环.(1-A-2-B).这个环有四条边.
现在把C ...

 | Version I: Can three houses be connected to three utilities concurrently, without the pipes crossing on any dimensional plane? Version II: Draw this puzzle on a piece of paper, and without lifting the pen from the paper or crossing lines, connect the utilities to the three houses. |

 A piece of paper with a hole in it is like a torus that has been squashed flat. This means that the three utilities problem can also be solved by cutting a hole in the center of a piece of paper. Lines are allowed to go around the sides of the paper, or through the hole to the other side.
A piece of paper with a hole in it is like a torus that has been squashed flat. This means that the three utilities problem can also be solved by cutting a hole in the center of a piece of paper. Lines are allowed to go around the sides of the paper, or through the hole to the other side.| Let's start by drawing lines from some of the utilities to some of the houses: gas -> house 1 -> electricity -> house 2 -> water -> house 3. |  |
| If we draw one more line, from house 3 to the gas company, then we have a loop. Notice that our loop has an inside and an outside. |  |
| That means two lines will have to be either outside or inside the loop. These two lines will have to cross. |  |
| That means the boundary of a face could either be house 1 - utility 1 - house 2 - utility 2 (four edges): |  |
| or house 1 - utility 1 - house 2 - utility 2 - house 3 - utility 3 (six edges): |  |

原帖由 caily 于 2007-9-9 08:25 发表
不是我这人直肠子,为得一个鼠标,出那么难的题,老吴你也太抠了。如果我这个答案有效的话,就把鼠标送我女朋友吧,我在剑桥先谢谢您了。嘎嘎嘎嘎
16904
这道题是英国最有名的谜题专家Henry Ernest Dud ...
原帖由 caily 于 2007-9-9 08:25 发表
不是我这人直肠子,为得一个鼠标,出那么难的题,老吴你也太抠了。如果我这个答案有效的话,就把鼠标送我女朋友吧,我在剑桥先谢谢您了。嘎嘎嘎嘎
16904
这道题是英国最有名的谜题专家Henry Ernest Dud ...
原帖由 pontifex 于 2007-9-7 13:15 发表
老吴还卖关子!我看不下去了!
1。http://www.supuzzle.com/supuzzle.html
这是题目的出处,是flash格式,可以在线玩。大家可以在线去玩玩!
2。http://mathforum.org/dr.math/faq/faq.3utilities.html
...

| 欢迎光临 鸿利在线|北京Thinkpad水货|IBM水货|Thinkpad笔记本|Thinkpad全球购|Thinkpad美行|Thinkpad水货笔记本|Thinkpad港行笔记本|Thinkpad T14|X13|P15|P17|P1隐士| X1 Carbon 9代 |T14S|2021款X1 Carbon|X1 隐士|Thinkpad非官方论坛|Thinkpad工作站|Thinkpad笔记本论坛|Thinkpad水货 (http://hongmz.cn:8989/) | Powered by Discuz! 7.2 |